I understand your suggested method and the benefits of some standardization with regards to ‘flex.’ The following is not an argument against anything that has so been posted. That aside, the variation suggested below is very similar to your test, differing only in its use of geometric centers, stagnation pressures, and moveable ‘foot’ posts.
First Approximation of Flex - Loading the Geometric Center
The test which I would like to suggest involves using the geometric center of the range of expected wetted surface area. Approximations of the geometric centers of various wetted areas can easily made, though not completely without some effort.
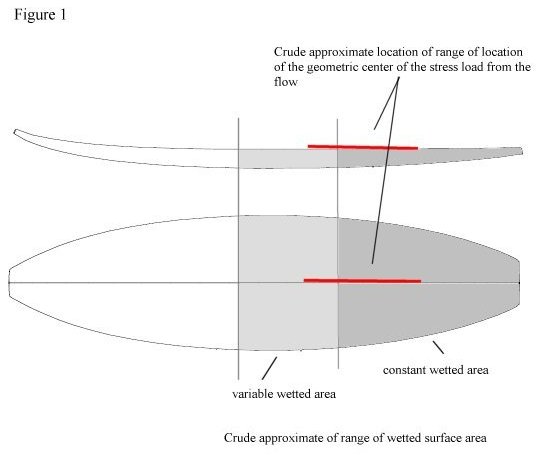
In Figure 1, I’ve used a handy close-tolerance blank outline to illustrate what is meant by geometric center – formally, it is the center of bottom wetted surface area in this case, and its calculation is analogous to that for the center of mass, or center of gravity.
I’ve indicated the wetted areas, which might interest me for instance. In as much, I’ve divided them up into variable and constant wetted areas. Using the total expected and then just the minimum (constant wetted area) you then establish a range of locations of the geometric center (as indicated in red.) The diagram is not meant to be accurate; it was created it for illustration.
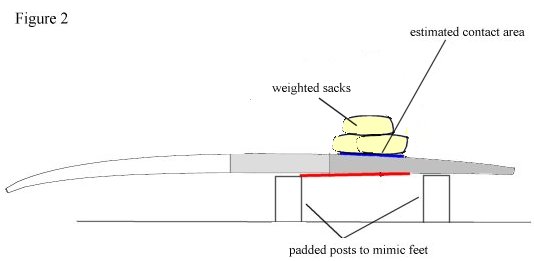
The geometric center can be considered the center of loading of the force arising from the flow in a wave –i.e. the stress load on the bottom. You simply flip the board, place your weight on the bottom surface somewhere on the red line, and then use either padded posts or blocks, each of which of similar, or of slightly larger surface than that of a foot, to mimic where a surfer might place his feet on the deck. See Figure 2.
As a first approximation to loading, I would use, stagnation pressure – a quick and dirty estimate of the pressure from a ‘head-on’ flow – which can be calculated using a simple formula. If you now know the wetted area, and a stagnation pressure, you therefore know the force. You can use weighted bags mimic the load, keeping them in roughly the same region as the geometric center. (It is possible to be more precise here, but going into at this point seems unnecessary.)
I understand that this appears to be more complex than your method, at least at first, as well as lacking the degree of standardization of your test - not to mention, it evolves math. Nevertheless, aside from attempting to control the geometric variablity, here are a few reasons why I think the method may have some merit.
-
All parameters of the test are easily communicated.
-
The force resulting from the flow is only communicated via the wetted surface –i.e. it is only the wetted surface that is in play, but it doesn’t exclude cases involving the whole board.
-
Using stagnation pressures is crude, but there is no restriction as to how much force can be applied, and you can work backwards if you know the force to water velocity.
-
Thought here I’ve used a symmetric case where the wetted area is rail-to-rail symmetric, it need not be - hence you can may be able to gauge ‘flex’ for any number of circumstances e.g. when the wetted area is asymmetric.
-
Though not apparent from the figure, the feet are moveable – back, forward, left and right.
When running the test, it obvious that measuring rail position before and after will likely go a long way.
Summary Notes
The measurement is a first approximation. The test model here is based on the assumption is that there would be a equilibrium between surfer/surfboard weight and load. That said, you could write volumes on what this kind of test isn’t going to tell you, and how it might be misleading. In particular, once you strain the structure, here the board, things change, i.e. it’s a crude first approximation.
kc